Time It Takes to Approach Steady State

Date published: 1 September 2020Tags: vibration

By Eric E. Ungar
Acentech, Inc., Cambridge, MA

Introduction

In dealing with a structure or a mechanical system that is subjected to a vibratory force, such as that due to a rotating machine, it is common in practice to consider only how the system responds in the steady state—that is, after the excitation has been applied for a considerable time.

In theory, reaching the steady state takes infinite time—the final steady state is never reached. But how long does it take to reach a given fraction of the steady state response?

Analysis Approach

Consider the classical simple mass-spring-damper system consisting of a mass m that is mounted to a rigid support via a parallel arrangement of a spring with stiffness k and a damper with viscous damping coefficient c, and assume that a sinusoidal force of amplitude F and radian frequency ω acts on the mass. For such a system, the displacement x of the mass m from its equilibrium position in terms of time t obeys the well-known differential equation

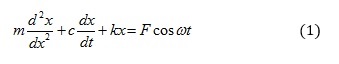
the complete solution of which consists of the sum of a steady-state component x_s(t) and a transient component x_T(t). One may obtain expressions for these components by following the usual analytical procedures. The mathematical steps are not presented here, but the results are summarized below.

The magnitude X_S of the steady-state component may be found to obey

with X_st = F / k denoting the static deflection of the mass due to a steady force of magnitude F and

Here β = ω/ω_n is the ratio of the radian frequency ω of the applied force to the system’s radian natural frequency:

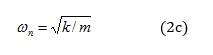
Also,

with the critical damping coefficient c_c given by

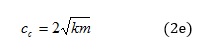
For the commonly considered case where the system is at rest and undeflected from equilibrium before the force is applied, one finds that the magnitude X_T of the transient component obeys

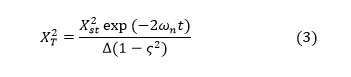
Thus, the ratio N of the magnitude of the transient component to the magnitude of the steady-state component is given by

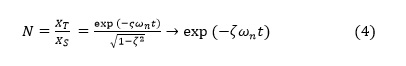
where the latter form is an approximation for the often considered practical case of small damping. Since the total motion consists of the sum of the steady-state and transient components, the total motion nears the steady state as the transient decreases—that is, as N becomes smaller.

Results and Observations

As evident from equation 4, the ratio N depends on the system’s natural frequency but not on the frequency of the excitation. Further, this equation implies that the time T_N it takes for the magnitude of the transient to decay to a given fraction N_c of the magnitude of the steady-state component obeys

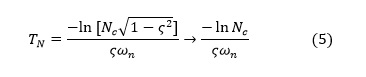
and that the number of cycles n_N it takes to reach the fraction N_c is

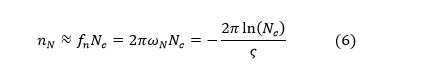
Note that n_N depends only on the value of the damping ratio.

For example, consider how long it takes for the response of a system with 3% of critical damping and a natural frequency of 15 Hz to reach 99% of its steady-state amplitude. This is the time it takes for the transient amplitude to decay to 1% of the steady-state amplitude and may be found here to amount to

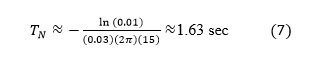
This corresponds to 1.63(15) = 24.4 cycles.

As apparent from equation 5, the time it takes for the transient to reach a given small fraction of the steady-state magnitude is shorter for (a) greater damping and (b) greater natural frequencies. This agrees with what one would expect since the transient motion is that of a system that is disturbed initially and then vibrates freely with decaying amplitude due to its damping.