Vibration Damping—Some Often-Overlooked Facts
By Eric E. Ungar
Abstract
“Damping” refers to loss of mechanical energy from a vibrating system, including dissipation into heat and transport of energy to adjacent structures and fluids. Thus, damping has an appreciable effect on only those mechanical system motions that are dominated by energy loss—for example, at resonances and during buildup or decay of forced vibrations. Viscous damping, with retarding forces proportional to velocity, is generally used for analyses because it leads to simple mathematical treatment; it may provide some guidance, but it represents reality in only a very limited range and may lead to erroneous results outside of that range. Structural damping, with retarding forces proportional to displacement, tends to provide better approximations to reality. Since damping may involve a multitude of mechanisms, it very rarely can be predicted on the basis of first principles and usually must be estimated, resulting in uncertainties in predicted damping-controlled motions.
1. Introduction
Although all professionals working in the field of noise and vibration control have an understanding of damping and its effects, it appears that many practitioners—even those with considerable experience—tend to harbor some misconceptions and may overlook some basic concepts. The purpose of the present article is to help remedy this situation. For the sake of simplicity and ease of explanation, I focus on simple models without drawing on the extensive analytical background available in the literature (Ungar and Zapfe 2006; Inman 2007).
2. Damping and Motions It Affects
“Damping” refers to energy dissipation—that is, to removal of mechanical energy from a vibrating system. In many instances the removed energy is converted to heat (e.g., via mechanical hysteresis in materials or external friction), but damping may also result from transport of energy from the system under consideration to other structural systems or to fluids.
Damping has an appreciable effect only on those aspects of a vibration that are controlled to a significant extent by energy dissipation. Consider, for example, the steady-state response of a sinusoidally excited simple mass-spring-dashpot system, as shown in the inset of figure 1. If the excitation is well below the system’s natural frequency, fn, then the applied force is opposed in essence only by the spring, and if the excitation is well above the natural frequency, the applied force is opposed essentially only by the mass. If the applied force acts in a limited range near the natural frequency, then the spring and the inertia forces in effect cancel out each other, and the response is controlled by the system’s energy dissipation capability.
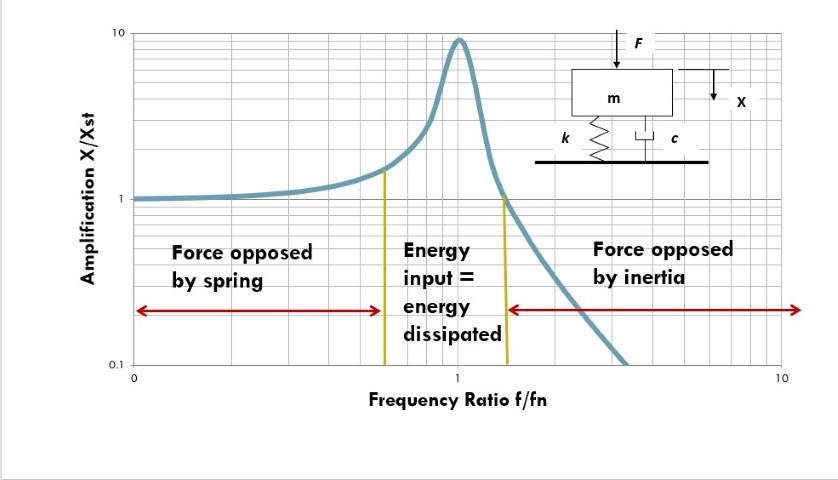
Figure 1. Domains of parameter dominances in steady vibration
In addition to controlling a system’s steady-state response at resonance, damping also controls the buildup of this response—that is, the rate at which the limiting value of this response is reached after an external force is applied. Similarly, damping controls the rate of decay of vibrations after an external force has ceased to act. Furthermore, damping controls not only vibrations produced by applied time-dependent forces but also so-called self-excited vibrations that are produced by steady forces interacting with system motions (e.g., friction-induced stick-slip vibrations of vehicle clutches and brakes and vibrations induced by fluid flows).
Damping also governs the decay of waves propagating freely along structures or in fluids. Moreover, it plays a dominant role in the response of platelike structures to incident sound and in the transmission of sound through walls—but only at frequencies above the coincidence frequency (the frequency at which the wavelength of free structural motions matches the wavelength in the ambient fluid) (Cremer and Heckl 1988, 247).
3. The Viscous Damping Model and Vibration Decay
Damping in a dynamic system classically has been modeled in terms of an element that provides a retarding force proportional to velocity, often diagramed as a dashpot (see inset in fig. 1). Such damping rarely corresponds to reality, but this model has come into wide use because it leads to equations that can be solved easily and because it yields some results that reasonably represent certain features of a system’s dynamic behavior.
The ratio c of retarding force to velocity is called the viscous damping coefficient. For viscous damping elements included in mass-spring-dashpot systems, such as that indicated in figure 2, it generally is convenient to work with the damping ratio ζ, defined as c/cc . The parameter cc is called the critical damping coefficient and is given by cc= 2√(km) in terms of the spring stiffness k and the mass m.
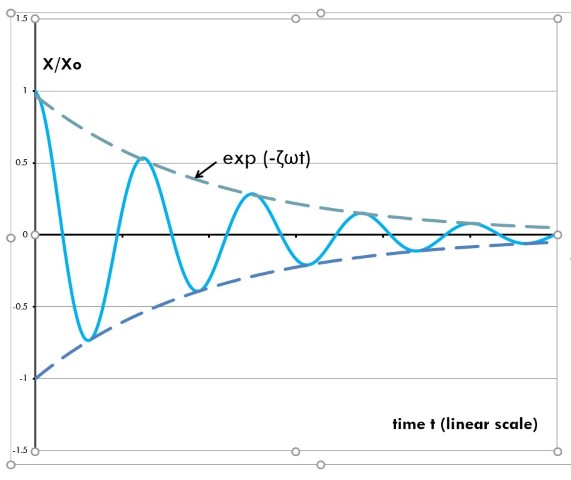
Figure 2. Vibration amplitude decay in system with viscous damping
As is known from classical analytical results, if the mass is deflected from its equilibrium position and released, it will vibrate with decreasing amplitude, as sketched in figure 2—provided that the viscous damping coefficient is not too large. If this coefficient is large enough, the deflected mass will drift toward its equilibrium position without oscillation. The critical damping coefficient cited above marks the dividing line between the two regimes; it is the smallest value of this coefficient for which oscillations do not occur.
A. Information from Vibration Decay Data
One may determine the value of the damping ratio, ζ, from a measured trace like that of figure 2 by considering the natural frequency, ω, of the system and making use of values obtained from the envelope of the oscillations. However, a plot of the logarithm of the (rectified) data versus time on a linear scale, as shown in figure 3, has advantages over a plot like figure 2. Not only does a logarithmic plot permit one to easily determine the damping ratio from the slope of the envelope, but observing the extent to which the envelope deviates from a straight line also enables one to determine how well the measured data corresponds to a simple viscously damped system. For example, if two damping mechanisms or modes are present, one may expect to obtain an initial decay with a steep envelope until the more effective mechanism’s action has been attenuated, followed by decay with a less steep slope associated with the less effective mechanism.
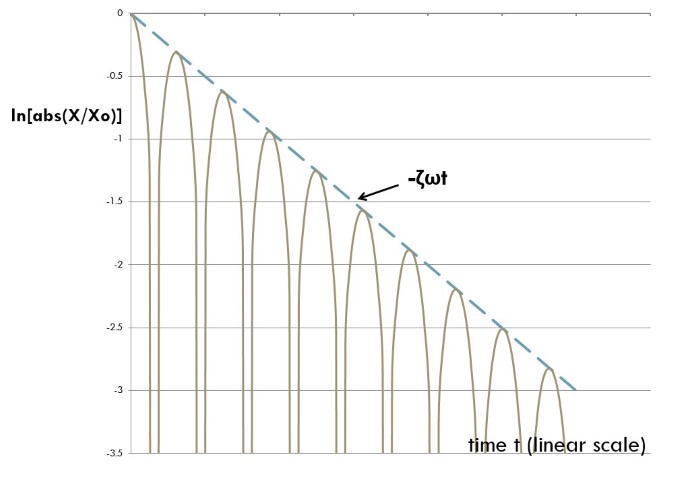
Figure 3. Decay of logarithm of amplitude in system with viscous damping
B. Decay of Vibrations Produced by Local Impacts
A commonly used approach for determination of the damping of the floor in a given area of a building consists of applying an impact to the floor in the area of interest and measuring the resulting decaying vibrations at a nearby point on the floor. (The impact often is applied by means of a “heel drop,” where a person stands on his or her toes and then lets the heels drop onto the floor.) Here and in other situations where damping is measured by observing the vibrations resulting from a local impact, the decay of the vibrations is due not only to energy dissipation in the local structure but also to energy propagation away from the measurement point, with the situation corresponding to that described above with two damping mechanisms present.
The damping that is determined from the early part of the decay curve, which often is considered as representative of the damping of the structure, may be expected to be due to both local dissipation and energy transport. Its use in practice may be fully appropriate if it represents the situation of interest—for example, in relation to evaluating the vibrations expected to be induced by a vibration source to be installed at the measurement location. However, damping evaluated from the early part of the decay curve would overestimate the structural damping; the damping magnitude deduced from the later part of the decay curve (obtained after most of the energy transport has occurred) is likely to better correspond to the structural damping.
4. Structural Damping—A Better Model
Because energy-loss considerations are of primary interest, it makes sense to characterize damping in terms of energy quantities. Perhaps the most widely used parameter used for such characterization is the loss factor η, defined for a steady vibration as the ratio of the energy dissipated per radian (or per cycle, divided by 2π) to the peak energy stored in the system under consideration. These quantities can be obtained as a function of frequency, amplitude, and temperature by direct measurements (Ungar and Zapfe 2006). Measured loss factor data for a wide variety of materials are available in the literature.
Whereas the viscous damping force is proportional to velocity, the “structural” damping force corresponding to a constant loss factor is proportional to displacement. It has been found that in many realistic cases, the loss factor varies little with frequency in the range of interest, so use of a constant loss factor results in more realistic description of a system response than use of a constant viscous damping coefficient. Figure 4, which is a plot of transmissibility (transmitted force/applied force) for a mass-spring-damper system, illustrates an effect of these two damping characterizations. The loss factor value (1.0) for the blue curve has been chosen so that the curve’s peak value is the same as that for the yellow curve, which pertains to the viscous damping coefficient of 0.5. Whereas the usually cited viscous damping model implies that greater damping increases the transmissibility at high frequencies (and thus reduces the effectiveness of an isolation system), the more realistic constant loss factor model implies that even a large amount of structural damping increases the high-frequency transmissibility only slightly above that obtained with zero damping.
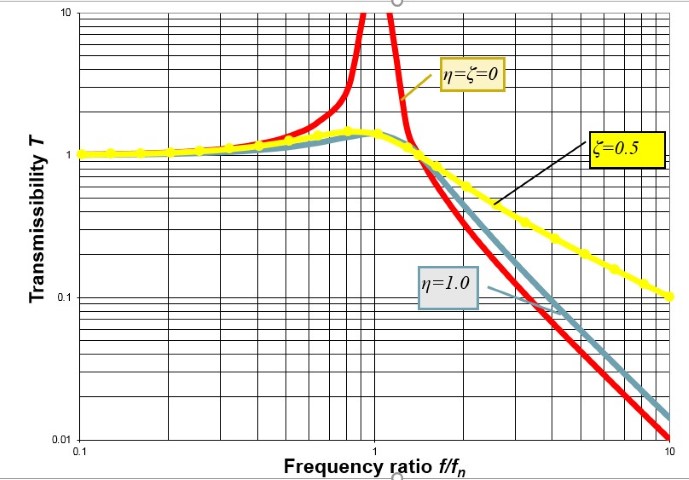
Figure 4. Comparison of viscous and structural damping effects on transmissibility
5. Damping Mechanisms and Estimation
Damping—loss of energy from a structural vibration—may occur via many different mechanisms. These include hysteretic processes in materials due to molecular and granular interactions or electrodynamic effects, as well as propagation of vibrations and sound to neighboring structures and ambient fluids. They also include friction between solids (including at structural connections and other interfaces) and viscous interactions with fluids.
It is important to note that all commonly used damping models, including viscous damping and structural damping (which is based on the cyclic energy loss), can provide realistic information concerning only the motion differences from one cycle to a subsequent cycle (or cycles) but cannot characterize the motions within cycles. For determination of details of the motions within cycles, such as those needed to characterize stick-slip processes, one requires complete and realistic descriptions of the involved physical mechanisms.
The multitude of mechanisms makes it generally impossible to predict the damping in practical structures on the basis of first principles. Only in cases where one damping mechanism is expected to dominate and that mechanism is amenable to analysis (e.g., where a viscoelastic coating is applied to a plate) can one expect to arrive at an approximate prediction.
In most realistic situations, the practitioner must estimate the expected damping, usually relying on experience, and thus is in the somewhat illogical position of predicting a structural response that is controlled by the structure’s damping on the basis of an estimated damping magnitude.
6. Concluding Remarks
One should keep in mind that damping is a measure of loss of mechanical energy and thus only has significant effects on motions dominated by energy dissipation.
Viscous damping, in which the retarding force is proportional to velocity, is the most often used damping model because it facilitates calculation. However, in many situations structural damping, in which the retarding force is proportional to displacement, gives more realistic results.
Data obtained from vibration decay measurements need to be evaluated carefully to account for the possible contributions from several modes and damping mechanisms.
Since damping in general results from the simultaneous action of several mechanisms, it generally cannot be modeled on the basis of first principles or quantified accurately. In practice its magnitudes are estimated on the basis of experience, thus injecting uncertainties into predictions of dissipation-controlled motions.
References
Cremer, L., and M. Heckl. 1988. Structure-Borne Sound. Berlin: Springer.
Inman, D. J. “Passive Damping.” 2007. In Handbook of Noise and Vibration Control, edited by M. J. Crocker, chap. 15. New York: Wiley.
Ungar, E. E., and J. A. Zapfe. 2006. “Structural Damping.” In Noise and Vibration Control Engineering, edited by I. L. Ver and L. L. Beranek, chap. 14. New York: Wiley.