What Happens at the “Critical” (Trace Matching) Frequency?
By Eric E. Ungar
Acentech, Inc., Cambridge, MA
Everyone who has studied sound transmission through walls and the like undoubtedly knows that much greater sound transmission occurs at frequencies above the so-called critical frequency than at lower frequencies. Why is that so? Descriptions and analyses abound in textbooks and handbooks, but it might be useful to take another look.
Trace Matching
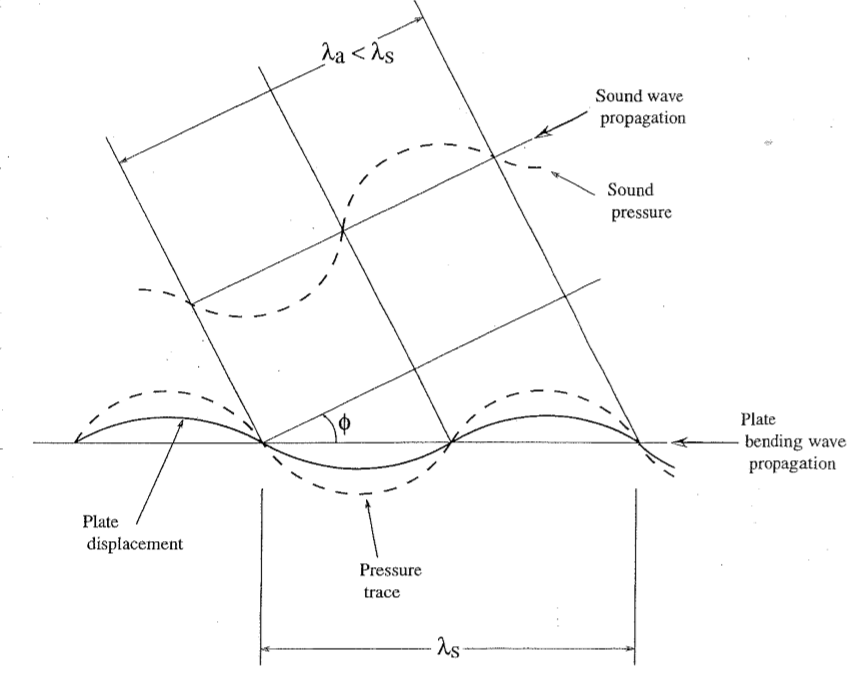
Figure 1 shows an on-edge view of a portion of an infinite plate separating two air volumes, in one of which (the upper one in the figure) there is a complex sound field. Let us focus on a component of that field that consists of a sound wave at a given frequency (and wavelength) and that impinges on the plate at a certain angle. Indicated in the figure is a one-wavelength long portion of that wave, together with the pressure distribution it produces on the plate, often called the “trace” of the sound pressure on the plate surface. Also shown is the deflection of the plate that this trace tends to produce. If the plate’s vibrational wavelength at the frequency of the sound wave matches the sound trace wavelength, then the sound pressure can deflect the plate very efficiently. In this “trace matching” case, the plate motion also can efficiently give rise to a sound wave propagating at the same angle in the second volume (the lower one in the figure). This transmitted wave is not diagrammed in the figure, but one can readily visualize the wave sketched above the plate continuing below the plate and recognize that good sound transmission can occur in the presence of trace matching.
Critical Frequency
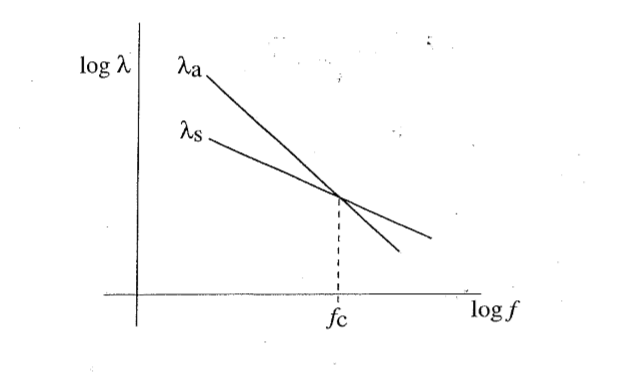
What are the conditions under which trace matching can occur? Note that in the diagram of figure 1, the sound wavelength λa is smaller than the structural wavelength λs. For any λa < λs one can find an angle φ at which the trace of the sound wave matches the structural wave. But if λa> λs, one cannot construct a diagram like that of figure 1, implying that trace matching cannot occur. Thus, λa = λs clearly constitutes a dividing line between good and poor matching of the pressure trace wavelength and the plate wavelength—and thus between good and poor sound transmission. The frequency corresponding to this dividing line—that is, to equality of the two wavelengths—is called the “critical frequency” or, more descriptively, the “trace matching frequency.”
As may be found, for example, in the classical book Noise and Vibration Control (L. L. Beranek, ed., McGraw-Hill, 1971), the acoustic wavelength at frequency f is given by λa = ca / f , where ca denotes the speed of sound in air. Also, the wavelength of flexural vibrations at frequency f of an infinite plate of thickness h and of a material with longitudinal wavespeed cL obeys
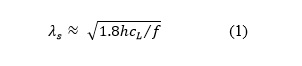
Thus, the frequency at which the two wavelengths match—the critical frequency—is given by
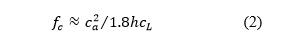
Figure 2 displays these frequency relations.
Infinite plates are hard to find, of course. But the vibrational behavior of a finite plate at frequencies that are high enough so that the plate length encompasses many wavelengths approximates that of an infinite plate. Note that the equation given above for the flexural wavelength on a plate is approximate in that it neglects the effect of Poisson’s ratio on the plate bending stiffness and includes rounding-off of the numerical values of the exact expression.
Broader Applicability
Although the foregoing discussion focused on plates in air, it applies equally to plates immersed in fluids with other sound-speeds—for example, water.
Furthermore, it also permits one to understand what happens if the fluids on the two sides of the plate are not the same—that is, if they have different sound-speeds—as in the case where there is air on one side of the plate and water on the other. In this situation, the angle at which there occurs efficient response of the plate to the sound field incident on one side will differ from the angle at which the plate radiates sound efficiently on the other side. This implies that there will be two different trace matching frequencies, one for each fluid, and good sound transmission may be expected at frequencies above the higher of these two. At these high frequencies, the angle of the incident wave will differ from the angle of the radiated wave.
It is interesting to note that the idea of trace matching frequencies applies not only to the response of plates to acoustic waves and to sound transmission through such plates but also to the transmission of other types of waves through other types of structures, such as the transmission of flexural waves on a plate past a reinforcing beam welded to that plate. (For example, see E. E. Ungar, “Transmission of Plate Flexural Vibrations through a Reinforcing Beam; Dynamic Stress Concentrations,” Journal of the Acoustical Society of America 33 [May 1961]: 633–639.)