Dynamic Absorbers—Another Look
By Eric Ungar
Acentech, Inc., Cambridge, MA
Introduction
All of us who work in the area of vibration control have some familiarity with dynamic absorbers (also called tuned dampers or neutralizers)—in essence, spring-mass arrangements that are attached to structures whose vibrations are to be reduced. But it may be useful to revisit absorbers and perhaps improve our understanding of just how and why they work.
Dynamic Stiffness
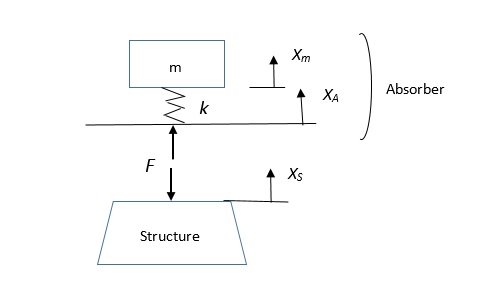
In simple terms, a dynamic absorber is a spring-mass system that is set in motion by a force that acts on the free end of the spring, shown schematically as the top part of the diagram in the attached figure. Let us focus on the situation where this force is steady and oscillates at radian frequency ω, making the point at which the force acts, as well as the mass, oscillate at the same frequency.
It is instructive to investigate the dynamic stiffness KA of the absorber since it is this stiffness that opposes the vibration of the structure whose motion is to be suppressed. This stiffness is defined as the ratio of the amplitude of the applied force F to the amplitude XA of the deflection of the point at which the force acts. Assuming the spring to be linear and massless, the mass to be rigid, and damping to be negligible (generally reasonable approximations to reality), one may find by application of Newton’s law that the dynamic stiffness of the absorber at the driving frequency ω obeys
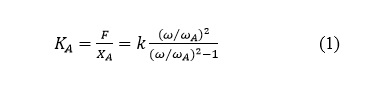
where ωA = √(k ⁄ m) denotes the radian natural frequency of the absorber. For the case where the force acts at a frequency that is much greater than the absorber’s natural frequency, this equation indicates that the dynamic stiffness KA is very nearly equal to the spring’s stiffness k. This happens because at high frequencies the inertia of the mass dominates, so that the mass moves very little and the applied force then basically only compresses the spring. For the situation where the force acts at a frequency that is much smaller than the absorber’s natural frequency, the foregoing equation indicates that the magnitude of the dynamic stiffness is nearly equal to mω2. In this domain, the inertia of the mass is so small that the spring is deflected very little and the applied force essentially only accelerates the mass.
At resonance of the absorber (that is, at ω = ωA), the dynamic stiffness becomes infinite in the absence of damping. In the presence of structural damping, the dynamic stiffness at resonance may be found to be given in terms of the structural damping factor η by
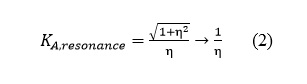
where the last term represents an approximation for small values of the damping. For the case of viscous damping, the η in this equation is replaced by 2ϛ, where ϛ is the ratio of the viscous damping coefficient to the critical viscous damping coefficient.
Extension of Absorber Spring
Since the dynamic stiffness is a measure of how much the absorber opposes to the force acting on it, one clearly wants in any practical application to make that stiffness as large as possible—that is, by choosing the absorber natural frequency to be at, or at least near to, the excitation frequency of concern.
However, the amplitude of the extension of the spring, ΔL, as measured from its static equilibrium condition, is directly proportional to the absorber’s dynamic stiffness. One may find that
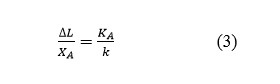
This implies that achievement of a high dynamic stiffness involves a large extension. In many practical cases, the space available to accommodate such extensions is limited, limiting the absorber stiffness that can be achieved.
Reduction of Structural Vibration Due to Absorber
Consider a vibrating structure (represented schematically by the trapezoid in the bottom portion of the figure) to which an absorber is to be attached at a given point and that the amplitude of the vibration at this point before the absorber is attached is XS. With the absorber (shown in the top portion of the figure) attached to the structure, the same force acts on the structure and on the absorber; also, the structure’s attachment point and the absorber move together with an amplitude XSA. This amplitude is smaller than the structure’s amplitude Xs without the absorber in place and depends on the absorber’s dynamic stiffness KA:
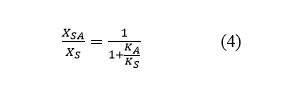
It is evident from this relation that achievement of reduction of the structure’s vibration by a sizable factor requires an absorber dynamic stiffness that is larger than the structural stiffness by a considerable factor.
Concluding Remarks
All I Really Need to Know I Learned in Kindergarten (Robert Fulghum, Villard Books, 1990) might be rephrased in the present context as “All I know about vibrations, I learned from linear mass-spring-damper models.” The foregoing discussion indeed is based on steady-state vibrations of such models that represent mathematically linear systems (with elastic elements whose stiffness does not depend on their deflection and with rigid mass elements). Such models can provide insights into the behavior of more complicated systems and also can serve as the basis for analyses of such systems, including arrangements of multiple absorbers attached to structures with multiple degrees of freedom (since their modes typically can be represented by equivalent spring-mass systems). Analyses based on these simple models in many cases can readily be extended to deal with nonlinearities such as these due to the deflection-dependent stiffnesses of spring elements and the nonrigidity of mass elements, as well as with transient vibrations.
Passive Vibration Control (Denys J. Mead, Wiley, 1998) and Vibration and Shock in Damped Mechanical Systems (John C. Snowdon, Wiley, 1968) discuss some multi-degree-of-freedom systems, address optimization, and suggest some practical applications—such as using a spring-supported battery as the absorber in a helicopter, supporting the engine in an earth-moving vehicle elastically so that it acts as an absorber, and adding small cantilevers with adjustable masses at their tips to obtain absorbers that can be tuned to suppress structurally radiated noise in aircraft cabins.